五大经典算法|3.分治法

分治算法（Divide And Conquer）把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。

分治算法的概念

在计算机科学中，分治法是一种很重要的算法。字面上的解释是“分而治之”，就是把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)……

任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。问题的规模越小，越容易直接求解，解题所需的计算时间也越少。例如，对于n个元素的排序问题，当n=1时，不需任何计算。n=2时，只要作一次比较即可排好序。n=3时只要作3次比较即可，…。而当n较大时，问题就不那么容易处理了。要想直接解决一个规模较大的问题，有时是相当困难的。

分治算法的思想

分治法的设计思想是：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

对于一个规模为n的问题，若该问题可以容易地解决(比如说规模n较小)则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。

如果原问题可分割成k个子问题，1<k≤n，且这些子问题都可解并可利用这些子问题的解求出原问题的解，那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。分治与递归像一对孪生兄弟，经常同时应用在算法设计之中，并由此产生许多高效算法。

分治法能解决的问题特征

  • 该问题的规模缩小到一定的程度就可以容易地解决
  • 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。
  • 利用该问题分解出的子问题的解可以合并为该问题的解；
  • 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

分治法解决问题的基本步骤

  • 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；
  • 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题；
  • 合并：将各个子问题的解合并为原问题的解。

经典例题

二分查找

在计算机科学中，二分搜索（binary search），也称折半搜索（half-interval search）、对数搜索（logarithmic search），是一种在有序数组中查找某一特定元素的搜索算法。

搜索过程从数组的中间元素开始，如果中间元素正好是要查找的元素，则搜索过程结束；如果某一特定元素大于或者小于中间元素，则在数组大于或小于中间元素的那一半中查找，而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空，则代表找不到。这种搜索算法每一次比较都使搜索范围缩小一半。

给定一个有序的数组，查找 value 是否在数组中，不存在返回 -1。

例如：{ 1, 2, 3, 4, 5 } 找 3，返回下标 2（下标从 0 开始计算）。

二分查找算法C语言实现代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include<iostream>
using namespace std;
int a[100]={1,2,3,5,12,12,12,15,29,55};//数组中的数（由小到大）
int k;//要找的数字
int found(int x,int y) {
    int m=x+(y-x)/2;
    if (x>y) { //查找完毕没有找到答案，返回-1
        return -1;
    }

    if (a[m]==k)
        return m; //找到!返回位置.
    else if (a[m]>k)
        return found(x,m-1);//找左边
    else
        return found(m+1,y);//找右边

}

int main(){
    cin>>k;//输入要找的数字c语言把cin换为scanf即可
    cout<<found(0,9);//从数组a[0]到a[9]c语言把cout换为printf即可
    return 0;
}

大数相乘

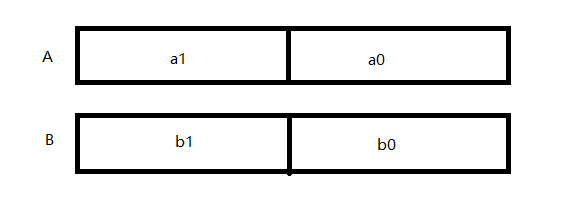
对于两个相同位数的大数A,B，且位数为2的整数次方，我们可以吧每个数按位数从中间分成两个数的和，如下图：
大数相乘
将A分成a1和a0， 将B分成b1和b0
普通的做法是A∗B=a1∗b1∗10n+(a1∗b0+b1∗a0)∗10(2/n)+a0∗b0A*B=a1*b1*10^n+(a1*b0+b1*a0)*10^(2/n)+a0*b0

举个例子：

1234∗9876=(12∗98)∗10000+(12∗76+98∗34)∗100+34∗761234*9876=(12*98)*10000+(12*76+98*34)*100+34*76

对于这个算法的时间复杂度，我们需要做4次n/2级别的乘法和3加法。即T(n)=4*T(n/2)+O(n),时间复杂度是O(n²）.

分治法的算法是A∗B=a1∗b1∗10n+[(a1+a0)∗(b0+b1)−a1∗a0−b1∗b0]∗10n/2+a0∗b0A*B=a1*b1*10^n+[(a1+a0)*(b0+b1)-a1*a0-b1*b0]*10^n/2+a0*b0

对于这个算法的时间复杂度，我们需要做3次n/2级别的乘法。即T(n)=3*T(n/2)+O(n),时间复杂度是T(n) = O(n^log2(3) ) = O(n^1.59).

分治法解决大数相乘问题的C语言实现代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
string multiply(string num1, string num2) {
	int init_len = 4;
	if (num1.length() > 2 || num2.length() > 2) {
		int max_len = max(num1.length(), num2.length());
		while (init_len < max_len)	init_len *= 2;
		add_pre_zero(num1, init_len - num1.length());
		add_pre_zero(num2, init_len - num2.length());
	}
	if (num1.length() == 1) {
		add_pre_zero(num1, 1);
	}
	if (num2.length() == 1) {
		add_pre_zero(num2, 1);
	}
	int n = num1.length();

	string result;

	string a1, a0, b1, b0;
	if (n > 1) {
		a1 = num1.substr(0, n / 2);
		a0 = num1.substr(n / 2, n);
		b1 = num2.substr(0, n / 2);
		b0 = num2.substr(n / 2, n);
	}
	if (n == 2) {
		int x1 = atoi(a1.c_str());
		int x2 = atoi(a0.c_str());
		int y1 = atoi(b1.c_str());
		int y2 = atoi(b0.c_str());
		int z = (x1 * 10 + x2) * (y1 * 10 + y2);
		result = to_string(z);
	} else {
		string c2 = multiply(a1, b1);
		string c0 = multiply(a0, b0);
		string temp_c1_1 = add(a0, a1);
		string temp_c1_2 = add(b1, b0);
		string temp_c1_3 = add(c2, c0);
		string temp_c1 = multiply(temp_c1_1, temp_c1_2);
		string c1 = subtract(temp_c1, temp_c1_3);
		string s1 = add_last_zero(c1, n / 2);
		string s2 = add_last_zero(c2, n);
		result = add(add(s1, s2), c0);
	}
	return result;
}

第K大数

在一个未排序的数组中找到第k大的元素，注意此言的第k大就是排序后的第k大的数，

总是将要划界的数组段末尾的元素为划界元，将比其小的数交换至前，比其大的数交换至后，最后将划界元放在“中间位置”(左边小，右边大)。划界将数组分解成两个子数组(可能为空)。

设数组下表从low开始，至high结束。

  • 1.总是取要划界的数组末尾元素为划界元x，开始划界：
    • a) 用j从low遍历到high-1(最后一个暂不处理)，i=low-1，如果nums[j]比x小就将nums[++i]与nums[j]交换位置.
    • b) 遍历完后再次将nums[i+1]与nums[high]交换位置(处理最后一个元素);
    • c) 返回划界元的位置i+1，下文称其为midpos.
      这时的midpos位置的元素，此时就是整个数组中第N-midpos大的元素，我们所要做的就像二分法一样找到K=N-midpos的“中间位置”，即midpos=N-K.
  • 如果midpos==n-k，那么返回该值，这就是第k大的数。
  • 如果midpos>n-k，那么第k大的数在左半数组.
  • 如果midpos<n-k，那么第k大的数在右半数组.
分治法解决第K大数问题的C语言实现代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
//思路首先：
//快排划界，如果划界过程中当前划界元的中间位置就是k则找到了
//time,o(n*lg(k)),space,o(1)
class Solution {
public:
    //对数组vec，low到high的元素进行划界，并获取vec[high]的“中间位置”
    int quickPartion(vector<int> &vec, int low,int high) {
        int x = vec[high];
        int i = low - 1;
        for (int j = low; j <= high - 1; j++) {
            if (vec[j] <= x)//小于x的划到左边
                swap(vec,++i,j);
        }
        swap(vec,++i,high);//找到划界元的位置
        return i;//返回位置
    }

    //交换数组元素i和j的位置
    void swap(vector<int>& nums, int i, int j){
        int temp = nums[i];
        nums[i]=nums[j];
        nums[j]=temp;
    }

    int getQuickSortK(vector<int> &vec, int low,int high, int k) {
        if(low >= high) return vec[low];
        int  midpos = quickPartion(vec, low,high);   //对原数组vec[low]到vec[high]的元素进行划界
        if (midpos == vec.size() - k) //如果midpos==n-k，那么返回该值，这就是第k大的数
            return vec[midpos];
        else if (midpos < vec.size() - k) //如果midpos<n-k，那么第k大的数在右半数组
            return getQuickSortK(vec, midpos+1, high, k);
        else  //如果midpos>n-k，那么第k大的数在左半数组
            return getQuickSortK(vec, low, midpos-1, k);
    }

    int findKthLargest(vector<int>& nums, int k) {
        return getQuickSortK(nums,0,nums.size()-1,k);
    }
};

循环赛日程表

设有n=2^k个运动员要进行网球循环赛。现要设计一个满足以下要求的比赛日程表：

  • (1)每个选手必须与其他n-1个选手各赛一次；
  • (2)每个选手一天只能参赛一次；
  • (3)循环赛在n-1天内结束。

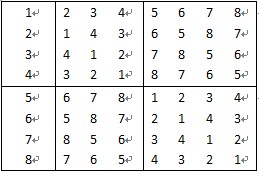
请按此要求将比赛日程表设计成有n行和n-1列的一个表。在表中的第i行，第j列处填入第i个选手在第j天所遇到的选手。其中1≤i≤n，1≤j≤n-1。8个选手的比赛日程表如下图：
循环赛日程表

按分治策略，我们可以将所有的选手分为两半，则n个选手的比赛日程表可以通过n/2个选手的比赛日程表来决定。递归地用这种一分为二的策略对选手进行划分，直到只剩下两个选手时，比赛日程表的制定就变得很简单。这时只要让这两个选手进行比赛就可以了。如上图，所列出的正方形表是8个选手的比赛日程表。其中左上角与左下角的两小块分别为选手1至选手4和选手5至选手8前3天的比赛日程。据此，将左上角小块中的所有数字按其相对位置抄到右下角，又将左下角小块中的所有数字按其相对位置抄到右上角，这样我们就分别安排好了选手1至选手4和选手5至选手8在后4天的比赛日程。依此思想容易将这个比赛日程表推广到具有任意多个选手的情形。

分治法解决循环赛日程表问题的C语言实现代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

#include <cstdio>
using namespace std;
int a[10000][10000];
void table(int k, int n) {
    for(int i = 1; i <= n; i ++) {
        a[1][i] = i;
    }
    int m = 1;  //每次填充起始位置
    for(int s = 1; s <= k; s++) {
        n/=2;
        for(int t = 1; t <= n; t++)  //分的块数
            for(int i = m+1; i <= 2*m; i++)
                for(int j = m+1; j <= 2*m; j++) {
                    a[i][j+(t-1)*m*2] = a[i-m][j+(t-1)*m*2-m];  //右下角的值等于左上角的值
                    a[i][j+(t-1)*m*2-m] = a[i-m][j+(t-1)*m*2];  //左下角的值等于右上角的值
                    //printf("i = %d\t j+(t-1)*m*2 = %d\t j+(t-1)*m*2-m = %d\t, i-m=%d\n", i, j+(t-1)*m*2, j+(t-1)*m*2-m, i-m);
                }
        m *= 2; //更新填充起始位置
    }
}
int main() {
    int k;
    cin >> k;

    int n = 1;
    for(int i = 1; i <= k; i++)
        n *= 2;
    table(k, n);

    for(int i = 1; i <= n; i ++) {
        for(int j = 1; j <= n; j ++) {
            printf("%d%c", a[i][j], j!=n?' ':'\n');
        }
    }
    return 0;
}
程序开发
五大经典算法 分治算法

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！